As tabelas de vida são usadas para descrever e entender a dinâmica populacional de uma espécie. Essa informação é importante nos estudos de conservação, agricultura, e saúde humana.

Usando a re-introdução de uma espécie como exemplo, as tabelas de vida podem indicar quando uma população reprodutiva fica estabelecida.

Há dois tipos de tabelas de vida, baseados no método de coleta de dados. Tabelas de vida específicas a idade começam com o que acontece a um cohort (grupo de indivíduos que nascem no mesmo período). Os membros do grupo pertencem a mesma geração e a população pode ser estável ou flutuante. Esse tipo de tabela de vida também é conhecido como tabela de vida horizontal.

As tabelas de vida específicas ao tempo se baseiam num cohort imaginário. Os pesquisadores coletam dados e determinam a estrutura etária para algum ponto de tempo. A premissa e que a população é estacionaria. As tabelas de vida específicas ao tempo também são conhecidas como tabelas de vida verticais ou estáticas.

Unidades de tempo usadas para mensuração de idade

Se a reprodução e sobrevivência são processos contínuos sem mudança cíclica, então qualquer unidade de tempo pode ser usado, dias, semanas, meses, ou  anos. As unidades de tempo devem proporcionar uma resolução boa. Por exemplo, se a longevidade de um organismo é de 2 anos, usando a unidade de 1 ano resultará em somente dois intervalos etários o que não é suficiente. Na maioria dos casos, o número de intervalos e idade varia de 10 a 50.

Se a reprodução e sobrevivência são cíclicas (ou sazonais), então um ciclo pode servir como unidade de tempo. Neste caso, pode ser que o número de intervalos de idade cairão a 2 ou 3. Porém, pode ser não limitante se a reprodução se restringe a um período curto dentro do ano porque não haverá muito diferencia de idades entre os organismos nascidos no mesmo ano.

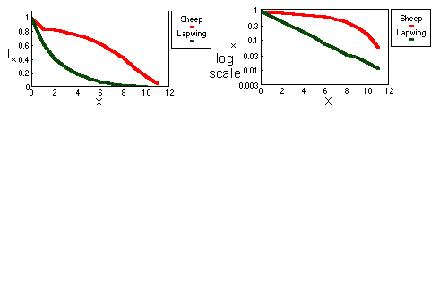
A curva de sobrevivência é exponencial (com crescimento negativo) para. Vanellus vanellus. Isso significa que a taxa de sobrevivência é independente da idade. Em escala logarítmica, a curva de sobrevivência  vira uma linha reta.

A mortalidade específica a idade é estimada usando a equação:

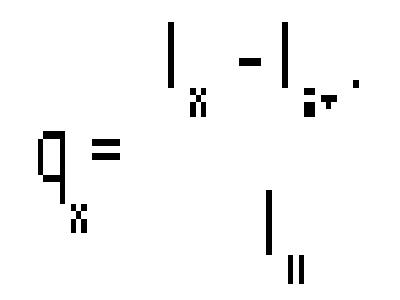
Características derivadas de tabelas de vida

Taxa de reprodução bruta, R0, é o  número médio de proles fêmeas nascidos  considerado na idade 0. Começamos com  N ovelhas recém nascidas. Algumas dessa morrerão sem produzir proles e outras produzirão várias proles. R0 é o número médio de proles fêmeas produzidos no grupo intero de  N ovelhas

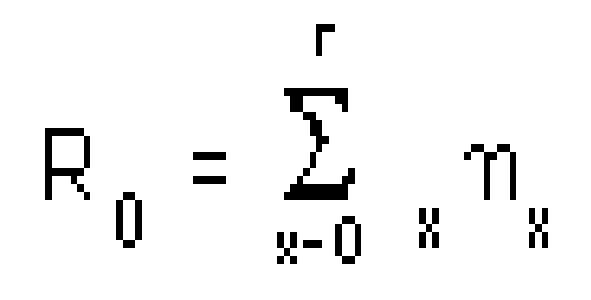
Para nosso exemplo, R0 = 1×0 + 0.845×0.045 + 0.824×0.391 + ... = 2.513. Ou seja, cada fêmea produz na média 2.513 proles fêmeas durante a vida.

Tempo médio de geração, T, é estimado usando a equação:

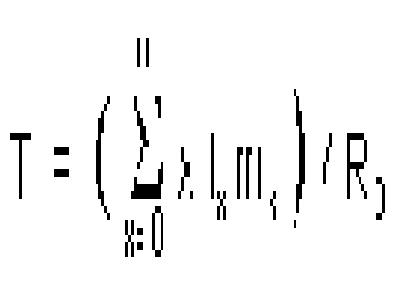
Observe: Se o organismo reproduz continuamente, então o tempo de geração será sobre-estimado usando essa equação porque  todos os nascimentos se adicionaram durante o período entre as datas do censo o que  é igual a uma classe de idade. O tempo de geração pode ser ajustado pela subtração da metade de uma classe de idade.

Pode estimar o valor aproximado da taxa de aumento  r usando essa lógica. Com a premissa de gerações discretas com tempo de geração de T=5.1 anos e uma taxa reprodutiva bruta de R0 =2.513. Se o tamanho populacional no tempo  zero é N0, então após T anos, a população crescerá até NT = N0×R0. De acordo com o modelo exponencial,

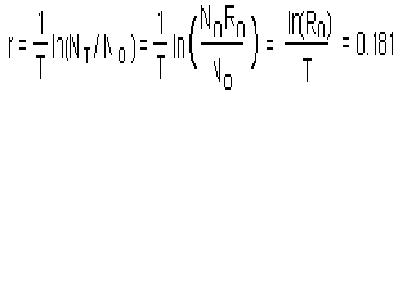
• Curvas de Sobrevivência

  As probabilidades de sobrevivência  lx freqüentemente se representam em gráficos por a idade x. Esses gráficos são "curvas de sobrevivência". Eles revelam a qual idade as taxas de mortalidade são baixas ou altas. Os gráficos a seguir demonstram curvas de sobrevivência  de ovelhas domesticas (dados de Caughley 1967) e para Vanellus vanellus na Grão Bretanha (dados de Deevey 1947):

 Os três tipos de curvas de sobrevivência.

Existem três tipos possíveis de curvas de sobrevivência (Figure 2). Uma curva de sobrevivência do tipo I se caracteriza por possuir a maior parte da mortalidade nos indivíduos mais velhos. Uma curva do tipo II tem uma taxa constante de mortalidade, e uma curva do tipo III tem mais mortalidade entre os jovens. O Homem em paises desenvolvidos tem uma curva de vida do tipo I.  A maioria de aves são de tipo II, e peixes, insetos e invertebrados marinhos se caracterizam por curvas de sobrevivência do tipo III.

Importante: Essa estimativa de r é aproximada  porque usamos uma premissa simplificada de que as gerações são discretas.

Estimando as taxas de reprodução (mx)

A taxa de reprodução é igual ao número de proles fêmeas produzidas por mãe no intervalo etário de  x a x+1. A sobrevivência das mães e proles durante esse intervalo de tempo deve ser incorporada a  m ; ou seja., mx ‘’e igual ao número total de proles produzidas num intervalo de tempo que sobrevivem até o fim desse período dividido pelo número inicial de mães no começo do intervalo do tempo.

Estimando a sobrevivência do organismo até a idade  x (lx)

Para os animais domésticos ou para populações criadas no laboratório, é possível observar o que acontece a um grupo grande de indivíduos que começaram a vida simultaneamente. Os sobreviventes podem ser contados em intervalos regulares do tempo e os valores de lx podem ser facilmente estimados. Uma técnica similar pode ser usada para organismos cesseis. É possível marcar um número grande de indivíduos e observar o que acontece com eles.

Esse tipo de análise geralmente não é possível para animais que se movimentam.  Existem dois métodos principais para deduzir os valores de  lx por determinar a distribuição etária da população ou por determinar as idades da morte.

Se a população não muda de números ou distribuição etária (estacionária) então o número de organismos recém nascidos há x unidades de tempo anterior são iguais a agora, e os sobreviventes deste grupo tem a idade x. Assim,

O método da estimação de  lx da idade de carcaças também requer a estabilidade do número na população e da estrutura etária.