Dependencia e Independencia da densidade

Para discutir a regulação de populações, podemos examinar a interação entre as forças dependentes da densidade (DD) e as forças independentes da densidade (ID) de uma perspectiva gráfica. Os gráficos terão N no eixo X e dN/dt mais as funções lineares no eixo Y.

Incorporamos as forças de DD por via das influencias logísticas do impacto da densidade da população sobre ela mesma. Anos "bons" de DD têm máximos maiores (acima da curva) e K maior (a distancia que a curva passa o eixo X, descrevendo N). Os anos "ruins" de DD têm máximos menores e K deslocado a esquerda. Incorporamos as forças de ID por via de funções lineares. ID forte (mais indivíduos retirados por um fator como clima ruim) implica uma tangente mais aguda.

A "moeda": medimos o impacto de DI e DD sobre o tamanho em equilíbrio da população, N*.

Têm-se fatores dependentes da densidade (DD) e independentes da densidade (ID) que influenciam a população de uma espécie. Usamos as características e premissas a seguir para modelar o sistema:

1) Se o fator da DD e a carga de predadores (cujo efeito per capita muda quando a população muda)
2) Se o fator da ID seja precipitação (com um efeito per capita que é constante independente do tamanho populacional).
3)Anos bons de DD terão cargas baixas de predadores, anos ruins de DD terão cargas grandes de predadores;
4) Anos bons de ID terão muita precipitação, anos ruins de ID terão pouca precipitação.
5) Assume que a variação da ID é tão grande ou maior do que a variação da DD.
6) Finalmente, assume que a carga de predadores (DD) e precipitação (ID) varia independentemente (ou seja, não estão correlacionadas).

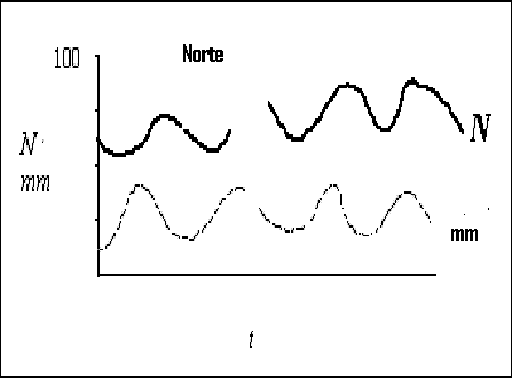
Variação do tamanho da população (N) e precipitação (mm) no tempo (t) para a população do norte. Preto, linha descontinua: precipitação, com uma média de aproximadamente 25 mm por ano, variando de aproximadamente 10 a 40 mm. No mesmo período de tempo, a população variou de aproximadamente 50 a 90 indivíduos, com uma média aproximada de 70. Observe que a população "segue" a precipitação – com um atraso menor.

Na população do norte, a precipitação proporciona um indicador bom da tendência da população. Pouco após de picos de precipitação ocorrem picos na população. [Dependendo da escala temporal (não especificada), pode implicar que a população responde com um atraso de um ano a mudanças na precipitação – pode ser porque levantamos "adultos" e números grandes desse ano representam o recrutamento no ano anterior].

A boa correlação da população do norte contrasta com a falta de correlação para a população do sul.

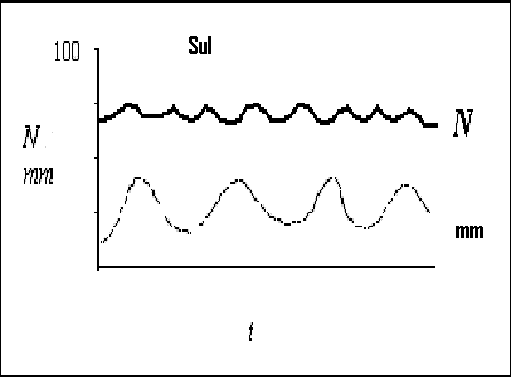
Variação da população (N) e a precipitação (mm) no tempo (t) para a população do sul. Preto, linha descontinua: precipitação, com uma média de aproximadamente 25 mm por ano, variando de aproximadamente 10 a 40 mm (a precipitação é igual nas duas localidades). Durante o mesmo período temporal a população demonstrou uma flutuação de aproximadamente 65 a 75 indivíduos, com uma média aproximada de 70. Note a precipitação tem correlação fraca com as tendências populacionais.

Por que a população do norte "segue" a precipitação, mas a população do sul não faz?

Termos curvas, representando os fatores intrínsecos dependentes da densidade (DD) (o efeito varia com a densidade: crescimento baixo com N baixo, a crescimento alto em valores intermediários de N, e depois diminua) por via o crescimento logístico.
Teremos linhas retas, representando os fatores independentes da densidade (ID) que afeita o crescimento populacional (ou seja afeita uma proporção constante da população). Deixamos que os fatores dependentes da densidade variem entre "bom" (curvas azuis com picos maiores, com uma K maior) e "ruim" (curvas azuis menores, com um valor de K menor). Os fatores independentes da densidade variam entre "forte" (tange maior, linha descontinua) e "fraca" (tangente menor, linha pontuada).

Podemos avaliar a diferencia entre o tamanho populacional em equilíbrio sob uma combinação de fatores reguladores versus outra combinação, para responder essa pergunta: "Qual diferencia é mais importante, as diferencias da ID (forte versus fraca) ou diferencias da DD (boa versus ruim)?"

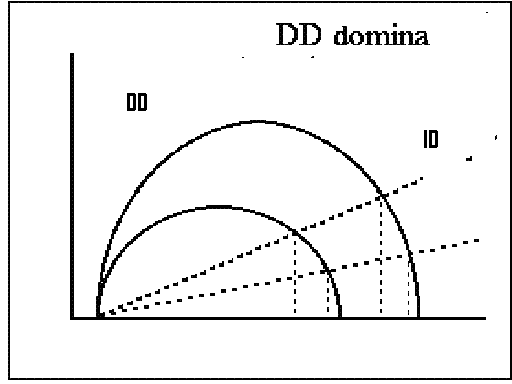
Interação entre os efeitos dependentes da densidade (DD) sobre o crescimento da população (curvas azuis continuas) e os efeitos independentes da densidade (ID) (linhas vermelhas descontinuas). A diferencia entre anos bons e ruins é grande para os efeitos de DD (diferencias a menos b e c menos d, mantendo os efeitos de ID constantes,comparada a diferencia entre os efeitos forte e fraco de ID (a menos c e b menos d, mantendo os efeitos de DD constantes). Os pontos a, b, c, e d representam o tamanho em equilíbrio da população – o tamanho em qual a adição (curvas azuis de DD do crescimento logístico) é balanceada pela subtração (curvas vermelhas descontinuas de ID da retirada independente da densidade). As quatro interseções da curva implica quatro pontos de equilíbrio.

Comparamos isso com outro caso onde os efeitos de ID são relativamente fracos (linhas na figura anterior) com um gráfico demonstrando efeitos mais fortes de ID,

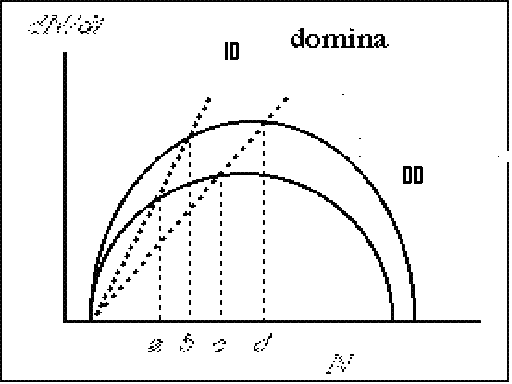
Interação entre os efeitos dependente da densidade (DD) sobre o crescimento populacional (curvas azuis continuas) e os efeitos independentes da densidade (ID) (linhas vermelhas descontinuas). Com linhas mais agudas de r ID, a importância relativa de DI e DD é trocado quando avaliamos os efeitos sob variação. A diferencia entre anos bons e ruins é agora grande para os efeitos de ID (a menos c e b menos d, mantendo os efeitos de DD constantes) comparado a aqueles dos efeitos de DD (diferencias de a menos b e c menos d, mantendo os efeitos de ID constantes).

Quais são algumas diferencias principais entre as forças atuando nas duas figuras anteriores?

1) No primeiro gráfico, a dependência de densidade é mais marcada (diferencia entre anos bons e ruins de K é maior)
2) No primeiro gráfico a independência de densidade é mais fraca (ambas as curvas têm uma tangente menor do que no segundo gráfico)
3) No segundo gráfico diminua a diferencia entre bom e ruim da DD.
4) No segundo gráfico aumenta o impacto dos fatores de DD (as linhas ficam mais agudas).

Usam-se a mesma notação para nomear os pontos como a, b, c, e d, então DD domina quando b > c, e ID domina quando b < c.

Resultado: DD domina no primeiro gráfico, e ID domina no segundo gráfico.