|
As equações básicas das quatro curvas (todos são tipos das
equações diferenciais dN/dt ):
DDboa =
rN(1-N/ Kboa)
DDruim =
rN(1-N/ Kruim)
IDforte = RforteN
IDfraca = RfracaN
Onde as primeiras duas são simplesmente
a equações logísticas – com um subscrito em K. Lembre do gráfico do logístico
dN/dt contra N i uma curve. As últimas duas equações são lineares (o intercepto de Y 0, á tangente é Ri, onde i ´pode ter
um efeito Forte, ou um efeito Fraco). Podemos considerar Ri como a proporção de indivíduos
retirados pelo fator da ID (esse fator da ID pode ser coleta, mortalidade devido ao clima, ou outra causa).
As quatro equações produzem as quatro curvas azuis ou vermelhas dos dois gráficos anteriores. Lembre, DD adiciona indivíduos,
e ID retira indivíduos.
As quatro curvas resultam em quatro
valores de N onde as curvas de DD
e ID intersectem – os pontos de equilíbrio. Usáramos o símbolo "&" para representar a interseção. IDforte & DDruin , por exemplo, implica
a interseção da linha de IDforte
e a curva de DDbom. Podemos resolver para N
na interseção dos pontos de equilíbrio ao formatar pares
de equações iguais entre elas. Os valores de N na interseção são:
a = IDforte & DDbom = Kbon [1-
(Rforte / r)]
b =
IDforte & DDbom = Kbom [1- (Rforte / r)]
c = IDfraca & DDbom = Kbom [1- (Rfraca / r)]
d
= IDfraca & DDbom = Kbom [1- (Rfraca / r)] As
interações de "trocar" são b e c. Sua magnitude relativa
determina determine se DD ou ID domina.
[Observe que a é sempre menor do que b, e c é sempre menor do que d, mas o
ordem de b e c pode variar].
Lembre que cada um desses é um ponto de equilíbrio
sob uma combinação de condições
Por que b e c importam (usando a como o ponto
de referencia
ID domina: If b < c então a a b (mudando DD e mantendo ID constante) é menor do que a a c (mudando ID
e mantendo DD constante)
Distancia pequena (a a b) implica que
o efeito da mudança de DD é pequeno
-- ID domina.
Distancia grande (a a c) implica que o efeito da mudança de ID é grande -- ID domina
DD domina: Se b > c então a a b (mudando DD e mantendo ID constante)
é mais comprido do que a a c (mudando ID e mantendo DD constante)
Distancia a a b grande implica
que o efeito da mudança de DD é grande -- DD
domina.
Distancia a á c pequena
implica que o efeito da mudança de ID é pequeno -- DD
domina
Questão: Se obtemos um "veredicto"
das distancias {a á c} e {a a b}, esses automaticamente implica
o veredicto das distancias {b a d} e {c a d}?
Voltamos à idéia do uso das diferencias
entre as interseções ID e
DD (a mudança nos valores de equilíbrio ao mudar as condições)
para decide qual domina.
O que significa a ordem de b e c?
Se b < c então a-b e c-d (mudanças de DD mantendo ID constante) são pequenas relativas a a-c e b-d (mudanças de ID mantendo DD constante). A mudança no tamanho em equilíbrio da população sob os valores de mudanças de ID é pequena relativa a mudança
do tamanho da população em equilíbrio para mudanças de DD
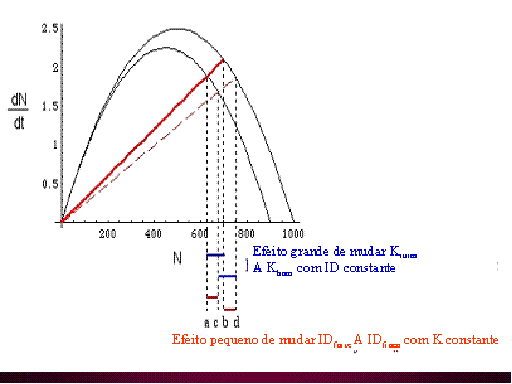 DD domina. {a a b}
e {c a d} grandes. Linhas descontinuas a-b,
c-d (etc.), Anotações de "efeito" proporcionam o contexto para
o sentido de ordem de b e c para ser comparado com o próximo gráfico.
ID domina Compare e contraste com o gráfico anterior. As barras horizontais vermelhas
e azuis abaixo o gráfica ilustram o efeito sobre N (medido no eixo
X) das mudanças dos efeitos de ID ou DD (dado pelas duas curvas e as duas linhas
vermelhas sólidas ou descontinuas). Ao aumentar a diferencia entre a linha sólida de IDforte e as linhas descontinuas IDfraco trocamos
a dominância de DD
a dominância de ID.
No
caso da variância pequena de ID o
efeito sobre N de mudanças de ID
é pequeno comparado ao de mudanças de DD.
As interações de "trocar" são b e
c. Sua magnitude relativa determina determine se DD ou ID
domina.
[Observe que a é sempre menor do que b, e c é sempre menor do que d, mas o ordem de b
e c pode variar]. Lembre que cada um desses é um ponto de equilíbrio sob uma combinação de condições.
Por que b e c importam usando a como o ponto de referencia
ID domina: If b
< c então a
a b (mudando DD e mantendo ID
constante) é menor do que a a c (mudando ID e mantendo DD constante)
Distancia pequena (a a b)
implica que o efeito da mudança de DD
é pequeno -- ID domina.
Distancia grande (a a c) implica que o efeito
da mudança de ID é grande --
ID domina
DD domina: Se b > c então a a b (mudando DD e mantendo ID constante)
é mais comprido do que a a c (mudando ID e mantendo DD constante)
Distancia a a b grande implica que o efeito da mudança de DD é grande -- DD domina.
Distancia a á c pequena implica que o efeito da mudança de ID é pequeno --
DD domina
Questão: Se obtemos um "veredicto" das distancias
{a á c} e {a a b}, esses automaticamente implica o
veredicto das distancias {b a d} e {c a d}?
Voltamos à idéia do uso das diferencias
entre as interseções ID e DD (a mudança nos valores de equilíbrio ao mudar as condições)
para decide qual domina.
O que significa a ordem de b e c?
Se b < c então a-b
e c-d (mudanças de DD
mantendo ID constante) são pequenas
relativas a a-c e b-d (mudanças de ID mantendo DD constante). A mudança no tamanho em equilíbrio da
população sob os valores de mudanças de ID
é pequena relativa a mudança do tamanho da população em equilíbrio para mudanças de DD.
DD domina. {a a b} e {c a d} grandes. Linhas descontinuas a-b, c-d (etc.), Anotações
de "efeito" proporcionam o contexto para o sentido de ordem de b e c para ser comparado com o próximo gráfico.
ID domina Compare e contraste com o gráfico anterior. As barras horizontais vermelhas
e azuis abaixo o gráfica ilustram o efeito sobre N (medido no eixo
X) das mudanças dos efeitos de ID ou DD (dado pelas duas curvas e as duas linhas
vermelhas sólidas ou descontinuas). Ao aumentar a diferencia entre a linha sólida de IDforte e as linhas descontinuas IDfraco trocamos
a dominância de DD a dominância de ID.
No
caso da variância pequena de ID o
efeito sobre N de mudanças de ID é pequeno comparado ao de mudanças de DD.
No caso da variância grande de
ID os efeitos de N são opostos
Examinamos duas técnicas para responder perguntas sobre
t ID versus DD. Uma técnica será numérica, e a outra será gráfica. Ambas compartilham várias características.
Com os dados a seguir
|
N* |
Intersecto |
|
630 |
IDfraca & DDruim |
|
495 |
IDforte & DDruim |
|
700 |
IDfraca & DDbom |
|
550 |
IDforte & DDbom |
N* é um dos quatro valores numéricos (eixo X)
da interseção entre uma curva de DD e ID. Os pontos
não estão em ordem nenhuma, mas você decide e explique se DD ou ID dominará.
Como resolver o problema? Nosso interesse é o efeito
(sobre N* o crescimento bruto esperado por DD - ID). Quais fatores
afeita o efeito? As curvas DD
e ID.
Efeito de X se Y fica constante vs. Efeito
de Y se X fica constante, nós deve informar qual é mais importante. Nesse caso, X e Y são
DD e ID.
Como avaliar o efeito? Podemos avaliar os efeitos como a diferencia entre bom e ruim, ou fraco e forte,
se o outro fator fica constante.
Sem ordem particular:
efeito de ID se DD
fica constante na curva de DDruim
: 630 - 495 = 135
efeito de ID se DD fica constante
na curva de DDbom :
700 - 550 = 150
Efeito de
DD se ID
fica constante na linha de IDforte: 550 - 495 = 55
Efeito de DD se ID fica
constante na linha de IDfraca: 700
- 630 = 70
Veredicto?
Os efeitos de ID (ambos > 100) são muito maiores do que
os efeitos de DD (ambos < 75), então ID domina.
Técnica gráfica:
Explique no gráfico a seguir qual fator domina:
Pergunta: dado esse gráfico, determine se DD ou ID dominará, e explicar seu raciocínio. [Resposta no próximo gráfico]
Podemos resolver
o problema mantendo as coisas constantes (ficando numa curva de DD ou uma linha de ID) e calculando diferencias
entre os tamanhos em equilíbrio (a a b, a a c, etc.) sob condições diferentes – mas o raciocínio agora
é gráfico.
Solução
da pergunta anterior. As linhas de queda [onde cruzam o eixo X nos informa do tamanho em equilíbrio da população] e uma explicação das
barra horizontais que as conectam forma uma explicação suficiente do resultado. Os efeitos da mudança de condições de
ID (barras vermelhas) i muito menor
do que o efeito de mudança nas condições de DD (barras azuis), então DD domina
|



